Every year of high school, Australian students learn about "mean", "median", and "mode".

Yet many people still get them mixed up. Perhaps some cats might help.

How much does a cat weigh?

This question is not so simple to answer because cats don't all weigh the same.

Suppose you also have seven cats and a bunch of scales to weigh them with.

How might we summarise our data into a single number that answers the question?

Mode

One option is just to choose the most common, or – we might say – the most fashionable weight.

The French word for fashion is mode. Here, fashionable cats wear pink berets and the mode is 4kg.

We might answer: "based on our data, cats typically weigh 4kg."

That's the mode.

Another option is to give the middle number – the median.

It's very important that we first arrange our cats in order. They might not like it!

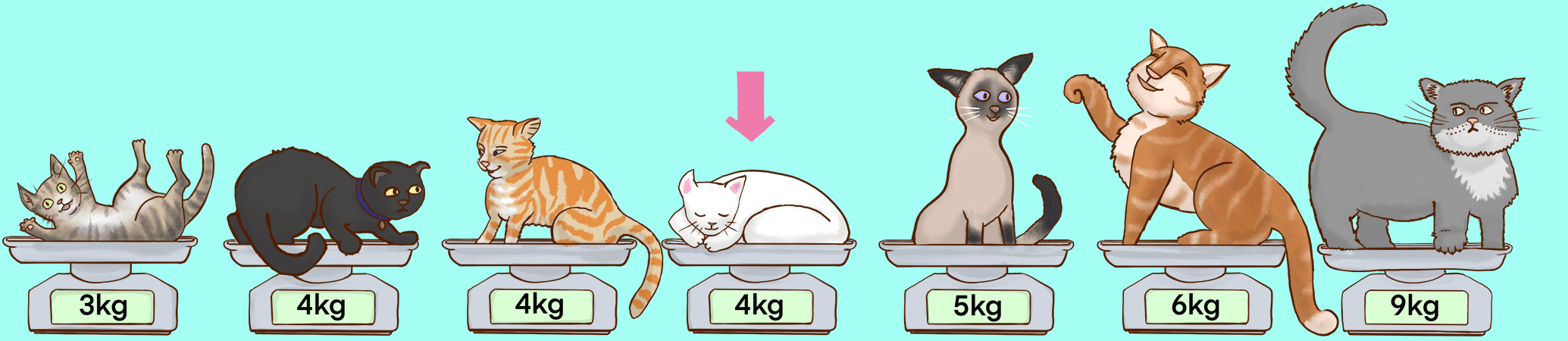
Now we choose the weight in the middle: 4kg. This is called the median. It splits our cats in two:

50% of the cats weigh less than or the same as the median.

50% of the cats weigh more than or the same as the median.

We might answer: "based on our data, cats weigh around 4kg."

That's the median.

Finally, we might be mean! We might pile all the cats onto one set of scales to find their total weight.

Then we can divide their total weight by the number of cats to get the mean:


        (5kg + 9kg + 6kg + 4kg + 4kg + 3kg + 4kg) ÷ 7 = 5kg

We might answer: "based on our data, cats weigh 5kg on average."

That's the mean.

So, there we have it. Three ways to summarise our data into a single number.

The mode: our most fashionable number:

the median: a middling cat that divides our data into two:

and the mean: where we cruelly weigh all our cats together and divide the total by the number of cats:

These are called summary statistics. Which is your favourite?